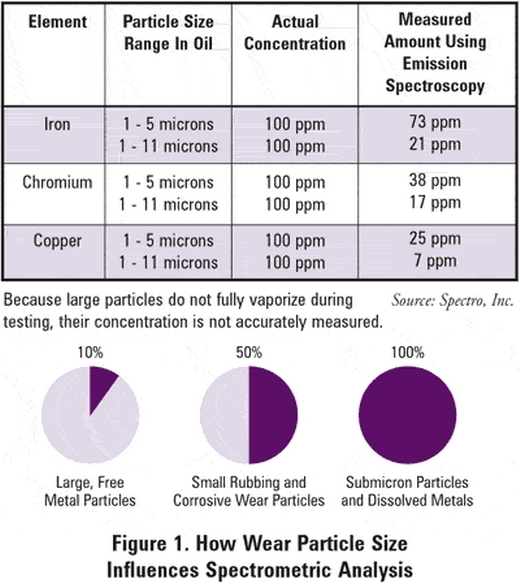
Yeah, I understand the concept just fine. IF you want to frame in in terms of accuracy vs precision, yes the precision model fits better:
with the embedded notation:
With regard to accuracy we can distinguish:
* the difference between the mean of the measurements and the reference value, the bias. Establishing and correcting for bias is necessary for calibration.
[like wear particle size/vaporization rate?!]
So, I may have some reservations on agreeing there.
ANYWAY, the debate afaik is accuracy verses
inaccuracy, you want to move the goalpost to make it a question of accuracy vs precision.
My definition of accurate is if I could predict the next set of wear numbers ~accurately~ if I have the previous set in hand. This seems sufficient for the sake of this argument. No need to make your overly complex arguments based more or less on rhetoric.
I also would like to invoke the basic principle of a more simple and direct analysis tends to yield the best results. Therefore, the application of common sense can make use of UOAs in the majority of cases to make general predictions about wear based on visc and service interval, just like Doug said. If you want to get him on this thread, fine, but it does not negate the entire UOA industry at large, lol.
I'm pretty sure that's where your argument leads, but you can clarify that, if you please.
While we wait....
http://en.wikipedia.org/wiki/Occam's_razor
Science and the scientific method
In science, Occam’s razor is used as a heuristic (rule of thumb) to guide scientists in the development of theoretical models rather than as an arbiter between published models.[5][6] In physics, parsimony was an important heuristic in the formulation of special relativity by Albert Einstein[15][16], the development and application of the principle of least action by Pierre Louis Maupertuis and Leonhard Euler,[17] and the development of quantum mechanics by Ludwig Boltzmann, Max Planck, Werner Heisenberg and Louis de Broglie.[6][18] In chemistry, Occam’s razor is often an important heuristic when developing a model of a reaction mechanism.[19][20] However, while it is useful as a heuristic in developing models of reaction mechanisms, it has been shown to fail as a criterion for selecting among published models.[6] In this context, Einstein himself expressed a certain caution when he formulated Einstein's Constraint: 'Everything should be kept as simple as possible, but no simpler.' Elsewhere, Einstein harks back to the theological roots of the Razor, with his famous put-down: 'The Good Lord may be subtle, but he is not malicious.'
In the scientific method, parsimony is an epistemological, metaphysical or heuristic preference, not an irrefutable principle of logic, and certainly not a scientific result.[7][8][9][10]
As a logical principle, Occam's razor would demand that scientists accept the simplest possible theoretical explanation for existing data. However, science has shown repeatedly that future data often supports more complex theories than existing data. Science tends to prefer the simplest explanation that is consistent with the data available at a given time, but history shows that these simplest explanations often yield to complexities as new data become available.[5][8] Science is open to the possibility that future experiments might support more complex theories than demanded by current data and is more interested in designing experiments to discriminate between competing theories than favoring one theory over another based merely on philosophical principles.[7][8][9][10]
One should note the related concept of overfitting, where excessively complex models are affected by statistical noise, whereas simpler models may capture the underlying structure better and may thus have better predictive performance. It is, however, often difficult to deduce which part of the data is noise (cf. model selection, test set, minimum description length, Bayesian inference, etc.)
The origins of what has come to be known as Occam's razor are traceable to the works of earlier philosophers such as Maimonides (1138–1204), John Duns Scotus (1265–1308), Thomas Aquinas (c. 1225–1274) and even Aristotle (384–322 BC) (Charlesworth 1956). The term "Ockham's razor" first appeared in 1852 in the works of Sir William Hamilton, 9th Baronet (1788–1856), centuries after Ockham's death. Ockham did not invent this "razor," so its association with him may be due to the frequency and effectiveness with which he used it (Ariew 1976). Though Ockham stated the principle in various ways, the most popular version was written not by him, but by John Ponce from Cork Ireland in 1639 (Meyer 1957).
The version of the Razor most often found in Ockham's work is Numquam ponenda est pluralitas sine necessitate, “For nothing ought to be posited without a reason given, unless it is self-evident (literally, known through itself) or known by experience or proved by the authority of Sacred Scripture.”[13] For Ockham, the only truly necessary entity is God; everything else, the whole of creation, is radically contingent through and through. In short, Ockham does not accept the Principle of Sufficient Reason.[13]
William Seach (c. 1285–1349) is remembered as an influential nominalist but his popular fame as a great logician rests chiefly on the maxim attributed to him and known as Ockam's razor: Entia non sunt multiplicanda praeter necessitatem or "Entities should not be multiplied unnecessarily." The term razor refers to the act of shaving away unnecessary assumptions to get to the simplest explanation. No doubt this maxim represents correctly the general tendency of his philosophy, but it has not so far been found in any of his writings. His nearest pronouncement seems to be Numquam ponenda est pluralitas sine necessitate [Plurality must never be posited without necessity], which occurs in his theological work on the Sentences of Peter Lombard (Quaestiones et decisiones in quattuor libros Sententiarum Petri Lombardi (ed. Lugd., 1495), i, dist. 27, qu. 2, K). In his Summa Totius Logicae, i. 12, Ockham cites the principle of economy, Frustra fit per plura quod potest fieri per pauciora [It is futile to do with more things that which can be done with fewer].
—Thorburn, 1918, pp. 352-3; Kneale and Kneale, 1962, p. 243.[12]